שלום כולם, וברוכים הבאים לאלישע והזוויות, עונה שניה פרק 4. היום ה-22 לאוגוסט 2024, י"ח אב תשפ"ד (טוב, זה לא. הקלטתי אתמול… עמכם הסליחה!)
בפרק הקודם עשינו את הקישור שבין בינה מלאכותית לבין יכולת למידה, ואמרנו שהיום נרים את מכסה המנוע ונראה באופן קצת יותר מפורט איך הדברים עובדים שם בפנים, בתוך הקופסה השחורה של מערכת לומדת שכזו. כמובן, זה לא פודקאסט טכני, אז המטרה שלנו בחיטוט הזה פנימה היא בעיקר לעבות את האינטואיציה שלנו לגביי המערכות הללו. כפי שתראו, מתוך ההבנה של איך הדברים עובדים בפנים, וגם מתוך השוואה לגישות אלטרנטיביות שנוסו לפני חמישים שנה, אנחנו נצא השבוע עם כמה תובנות עומק על הפוטנציאל הגלום במערכות הללו, לצד האתגרים שיש בעבודה איתן. ספיציפית, אני רוצה שבסוף הפרק הזה תהיה לכם לפחות תשובה חלקית לשאלה: למה קשה לנו להסתכל בתוך המערכות הללו ולענות על השאלה - האם יש שם תבונה?
הרבה פעמים קל יותר לדבר על דברים כשיש לנו דוגמה קונקרטית ביד, ולכן בפרק הזה אנחנו נשתמש בעיקר במערכת דמיונית שנקרא לה "החתוליה". המערכת הזו מספקת שירות פשוט: מקבלת כקלט תמונה דיגיטלית, ומוציאה כפלט קביעה - האם יש או אין בתמונה הזו חתול.
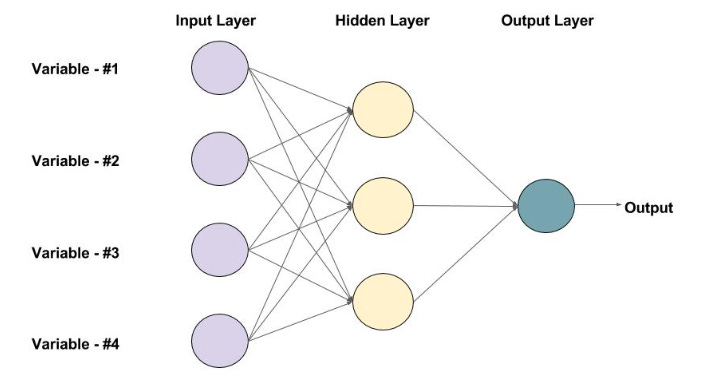
מערכות כאלו מבצעות את הפעולה שלהן לרוב על ידי תוכנה, אבל יותר קל לדמיין אותן דווקא כמשהו פיזי, קופסה שחורה פיזית שמונחת לנו על השולחן, כשהקלט נכנס מצד שמאל, והפלט יוצא מצד ימין. מה קורה בין קבלת הקלט לבין הוצאת הפלט? אם השירות הזה נבנה על פי הארכיטקטורות המקובלות היום, אז כשנפתח את הקופסה נגלה שבתוכה יש הרבה רכיבים קטנים, קופסאות שחורות קטנות יותר, שגם הן מקבלות קלט ומוציאות פלט. כדי להבחין בינן לבין הקופסא כולה, בואו נקרא להן "רכיבים" בהמשך הדיון. הרכיבים הללו מאורגנים בשכבות, והמידע זורם בהם משמאל לימין: הקלט הראשוני נשלח לכל הרכיבים שבשכבה הראשונה, והפלט של רכיבים אלו נשלח לרכיבים בשכבה השניה, וכן הלאה וימינה עד שזה מגיע לשכבה האחרונה ויוצא החוצה עם תשובה למשתמש.
אתם בטח רוצים לדעת - מה עושה כל אחד מן הרכיבים הללו? בגדול, מה שקורה כאן הוא שכל רכיב כזה עובד רק על חלק קטן מהבעיה, ומעביר את התוצאות מהניתוח שלו הלאה. לצורך ההמחשה בלבד, אפשר לדמיין את זה ככה: כדי למצוא חתולים בתמונות, אז אולי אחד הרכיבים עסוק בלחפש עיניים של חתול, ורכיב אחר עסוק בלחפש זנבות חתולים, וכן הלאה, ובשכבות מתקדמות יותר יש רכיב שצריך לשלב את כל המידע מהשכבות הקודמות כדי להגיע להחלטה, יש או אין חתול. בשלב הזה בעונה, אני לא חושב שכדאי שנפתח את תיבת הפנדורה שצוללת לתוך איך הרכיבים עצמם עובדים, ועדיף שנישאר ברמת הרזולוציה שהגדרנו כאן: יש לנו מערכת שמפמפמת מידע משמאל לימין, מעבירה אותו כמה שלבים של עיבוד בין רכיבים מדורגים, כשכל שלב בעיבוד יכול לקבל כקלט את התוצרים המעובדים של השלבים שקדמו לו. ולסיום הפירוט הזה אני רוצה גם לספר לאלו מכם שלא מגיעים מהתחום, שכשאתם שומעים על משהו בשם "רשת נוירונים" - מתכוונים בדיוק למערכת מהסוג שתיארתי כאן, לפחות בגרסתה הפשוטה ביותר.
עם המבנה הזה בראש, בואו נקשר את זה לדדוקציה ואינדוקציה שדיברנו עליהן בשבוע שעבר. כפי שאתם זוכרים, דדוקציה זו הפעלת הכללים שמוטמעים במערכת על קלט חדש, וזה בדיוק מה שתיארנו כרגע. מגיעה תמונה, היא נכנסת משמאל, עוברת ניתוח בשכבה הראשונה, משם לשניה וכן הלאה דרך כל השכבות, עד שהמערכת מוציאה בסוף תשובה למשתמש. לדבר הזה קוראים, במונחים של מדעי המחשב Forward Propagation, פיעפוע קדמי, כשהמילה forward פה מרמזת על כך שהתנועה היא קדימה, משמאל לימין, מן הקלט אל הפלט.
לעומת זאת, בשלב האינדוקציה, אנחנו רוצים ללמוד את הכללים. איך זה קורה? ובכן, כאן יש תהליך כפול. מתחילים באותו תהליך של פיעפוע קדמי, מסתכלים על התשובה שקיבלנו בסוף, ובודקים אם המערכת צדקה. בואו נניח שהיא טעתה - נניח אמרה שאין חתול בתמונה כשבעצם יש שם חתול. במקרה כזה אנחנו נותנים לה משוב, ואומרים לשכבה האחרונה - "טעות! יש כאן חתול! את צריכה לתקן את הכללים שלך כדי להכריע באופן מדוייק יותר על קלט שכזה".
עכשיו, השכבה האחרונה הזו אומרת לעצמה: "אוקיי, אולי טעיתי בשיקול הדעת שלי, אבל יכול להיות גם שהבעיה היא במה שקיבלתי מהשכבה הקודמת. אולי שם היתה טעות. נניח, השכבה הקודמת אמרה לי שיש בתמונה עינים חתוליות בפינה השמאלית העליונה, אבל אולי אין כאלו". בשל המצב הזה, השכבה גם מבצעת אצלה, מקומית, תיקונים, וגם מספרת לשכבות שקדמו לה - "היי, עשינו טעות, בצעו בדק בית ושפרו ביצועים". וכך זה ממשיך אחורה ואחורה במערכת, כשכל שכבה גם מבצעת התאמות אצלה וגם מעבירה את המשוב לשכבה שלפניה. לתהליך הזה קוראים Back Propagation, פיעפוע אחורי, ונראה לי שברור לכם מה הסיבה: התנועה כאן היא הופכית, מהפלט אל הקלט.
יש לנו הרבה מה להעמיק במערכות הללו, אבל כבר מתוך התהליך שתיארתי כאן עולה משהו מעניין: המערכות הלומדות הללו הינן מערכות מבוזרות, כשכל רכיב רק רואה חלק מהתמונה המלאה, וממילא קשה למקד איפה בדיוק ההחלטה לגביי החתול נעשית. והאמת, שווה לומר שיש עוד מערכות בעלות אופי דומה בעולם, כמו נניח מערכות של ביורוקרטיה ממסדית. דמיינו שאתם רוצים לקבל אישורי בנייה לאיזשהו משהו גדול, נניח איזה קניון. זה בוודאי דורש הרבה אישורים בירוקרטיים, הרבה אישורים בכל מיני רשויות, רשויות מקומיות, רשויות ארציות, בדיקות של תברואה, בדיקות של פגיעה במאגרי מים וטבע וכן הלאה וכן הלאה. אז אתם מגישים בקשה, וכל אחת מן הרשויות בוחנת את הבקשה מהזווית שלה, ומעבירה את המסמך שהיא חתמה עליו לרשות אחרת, וכן הלאה וכן הלאה, עד שזה מתנקז להחלטה מרוכזת אחת. גם כאן יש לכל רשות פרספקטיבה מקומית בלבד על הסיפור, וגם כאן אם תערערו על ההחלטה הסופית תצטרכו לעקוב אחרי מסלול הניירת מהסוף להתחלה כדי לגלות איפה התגלעו בעיות בבקשה שלכם.
אז אפשר לחשוב על מערכות לומדות כמו שלנו באופן הזה, משרדים ביורוקרטיים שמעבירים ביניהם מסמכים כדי להחליט החלטות, רק שבמקום תקשורת מסמכולוגית, הרכיבים שלנו מתקשרים במספרים, המון מספרים, וגם הכללים שהם לומדים ומפעילים הם נוסחאות מתמטיות וסטטיסטיות. בפרק הבא אנחנו נדבר קצת על מה בדיוק המספרים הללו מייצגים, ובינתיים אנחנו נמשיך הלאה.
מבין שני התהליכים, אינדוקציה ודדוקציה, נראה שהחלק של הדדוקציה הוא החלק הקל. הכללים כבר שם, נכון? רק צריך להפעיל אותם. שלב הלמידה, לעומת זאת, הוא מאתגר יותר: איך מלמדים מחשבים? אנחנו מדברים כאן על למידה מתוך ניסוי וטעיה, אבל לפני כחצי מאה, בעיקר בשנות השבעים והשמונים, היתה גישה אחרת לכך מאשר הגישה האינדוקטיבית. בתחום שלם שנקרא "מערכות מומחה" - Expert Systems - רצו ללמד מחשבים את הכללים באופן ישיר ומפורש, ולא להזדקק בכלל לשלב האינדוקציה.
גם כאן, אפשר וכדאי לשאוב אינטואיציה מבני אדם. בני אדם אמנם יכולים ללמוד על ידי ניסוי וטעיה, אבל יש להם גם מסלול עוקף אינדוקציה: הוראה על ידי מישהו אחר. רובנו למדנו כשהיינו קטנים שאסור לגעת באש, אבל אם התמזל מזלנו למדנו את זה לא על ידי ניסוי וטעיה. אלא ההורים שלנו אמרו לנו לא לעשות את זה, ואולי גם הסבירו למה, ולכן לא עשינו את זה. כשמורה מלמד אותנו קורס פיזיקה באוניברסיטה, הוא בעצם חוסך לנו הרבה זמן של למידה אינדוקטיבית בכך שהוא מספק לנו את הכללים, את הנוסחאות - את כל התובנות שאנשים אחרים ירקו דם כדי לגלות ולנסח. לפעמים נידרֶש לבדוק שהנוסחאות נכונות באיזו מעבדה, אבל את הכללים מישהו אחר גילה וניסח, ואנחנו מקבלים אותם כנתון ופועלים על פיהם. כפי שאמר ניוטון - אם ראיתי למרחוק, זה בגלל שעמדתי על כתפי ענקים. כלומר, אצל בני אדם תיתכן למידה על ידי העברת ידע קיים לאנשים חדשים באופן מפורש, והטמעה שלו באופן ישיר במוחם של הלומדים, בלי שהם צריכים לעבור את תהליך האינדוקציה באופן עצמאי.
ואכן, זה היה הרעיון מאחורי הרבה מערכות המומחה שהזכרתי קודם: בואו נכתוב תוכנה שבה, במקום שאיש התוכנה יגדיר את הפעולות שצריך לעשות, התוכנה תאפשר לאיש מקצוע בָּתְחום הרלוונטי להכניס בעצמו את הכללים למערכת. בשנות ה-60 וה-70 נבנתה מערכת בשם Mycin שהתמקדה בדיאגנוזה של מחלות מִדבקות, ומערכת בשם Dendral שהתמחתה בזיהוי מרכיבים כימיים לחומרים לא מזוהים. עוד דוגמה יש לנו ממאמר בשנת 1986, שבו השתמשו במערכת בשם APES כדי להטמיע במחשב את הוראת החוק הבריטי שקובע מיהו אזרח בריטי. ולא רק שהמערכות הללו פותחו, אלא שבשנות ה-80, כשהמערכות הללו היו חזית הטכנולוגיה, הרבה אנשים היו בטוחים ששם טמונה ההבטחה של ה-AI. עם מספיק מאמץ והשקעה, כך חשבו, נוכל לבנות מערכות שכאלו, להעביר להן את כל הידע האנושי, וכך נקבל רופאי-על ממוחשבים, עורכי-דין מטאוריים עשויים מסיליקון, וכן הלאה.
אולי חלקכם אומרים לעצמכם: רגע, למה שזה בכלל ייחשב AI? פעם, מתכנתים כתבו את החוקים של התוכנה, ובתוכנות הללו שתיארת כאן המתכנתים פשוט מעבירים את השרביט למישהו אחר שיכתוב את הכללים. אתם יכולים לקרוא לכתיבה הזו של החוקים מה שתרצו, אפילו "למידה", אבל במה התוכנה הסופית שונה מתוכנה רגילה? רק הגמישות המקדמית של התוכנה?
השאלה הזו מצויינת, ולכן שאלתי אותה! אני רוצה לענות עליה בשתי רמות. קודם כל, תמיד צריך לחזור לטיורינג היקר שלנו: לפי מבחן טיורינג, לא מעניינת אותנו שאלת המימוש, שאלת ה"איך זה בנוי". כל עוד זה מסוגל לעבור את מבחן טיורינג, מבחינת טיורינג זהו מכשיר תבוני. ובמקרה שלנו, מערכת APES שהזכרתי, שיכולה לענות על שאלות בתחום החוק הבריטי, יכולה אולי לעבור סוג של מבחן טיורינג מצומצם, כזה שמוגבל לשאלות ששואלים עורכי דין מומחים בתחום. אז אף אחד לא חשב ש-APES עוברת את מבחן טיורינג, אבל אפשר להבין למה חשבו שזה צעד בכיוון הנכון. זו סיבה אחת.
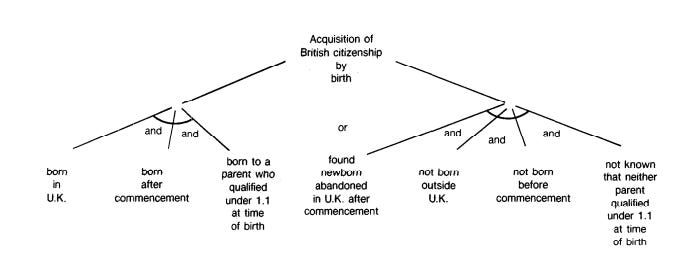
מעבר לזה, ישנה גם סיבה עמוקה עוד יותר שמצדיקה את החשיבה לפיה תוכנות כאלו יכולות להפוך עם הזמן למשהו אינטלגנטי יותר מתוכנה קלאסית. הסיבה הזו היא שהתוכנות הללו התאפיינו בכמה יכולות חדשות שלא היו לתוכנות קלאסיות, שנראו כאילו הן מתקרבות לחשיבה אנושית. לצורך הדיון בואו נתמקד בתוכנת APES שמכילה את הכללים על אזרחות בריטית. יכולות הדדוקציה של התוכנה איפשרו לה לקבל מקרים מעניינים וחדשים שמעולם לא ראתה, לקבוע מה עמדת החוק לגביהם, או להתריע על סתירות מסעיפים שונים בחוק כמו גם על חורים בחוק. לדוגמה, אם החוק קובע שמישהו הוא אזרח בריטי רק אם אחד ההורים שלו היה אזרח בריטי בעת לידתו, מה יאמר החוק במקרה של תינוק עזוב שנמצא ברחוב ללא תעודת זהות? על ידי הפעלת הכללים הקיימים באופן אוטומטי במחשב, אפשר לגלות יחסית בקלות אם המקרה הזה מכוסה בכלל בחוק.
דבר עוד יותר מגניב שאפשר היה לעשות, היה להתחיל מתוצאה מסויימת ולשאול את המערכת - האם יש מקרים שיובילו לתוצאה הזו. בעצם מה שנדרש כאן היה להפעיל את הכללים מהסוף להתחלה - לומר, "אם מישהו הגיע למעמד אזרחי X, זה יכול היה להיגרר רק מסעיפים א–ד בחוק, שהם יכולים להיווצר רק בסיטואציה 7". דברים מהסוג הזה היוו קפיצת מדרגה מבחינת יכולות לוגיות של מחשבים, קפיצה שהרגישה כמתקרבת יותר לעולם של חשיבה אנושית רציונלית. וכאן, אני רוצה לקוות, אתם מבינים איך זה גם מתקשר לתחילת הפרק. שכן לתהליך הראשון של בחינת מצב נתון ובדיקה מה החוק קובע לגביו קראו אז forward chaining, שרשור קדמי, ולתהליך השני של ספקולציה על מה יכול לגרום לתוצאה מסויימת קראו - backward chaining, שרשור אחורי. שמים לב לדמיון עם המונחים back and forward prop? זה לא סתם, אלא אותה אינטואיציה: באחד אתה מפעיל כללים קיימים על מקרה נתון, בעוד בשני אתה מקבע תוצאה מסויימת ובודק אם הכללים מסוגלים להכיל אותה ובאילו מקרים היא תתממש. גם במערכות הללו אפשר היה למדל את ההתנהגות שלהם כמו רכיבים קטנים של לוגיקה שמופעלים בשני הכיוונים. מה שהיה חסר למערכות הללו היה היכולת ללמוד - לא היתה שום דרך לעדכן באופן אוטומטי את הכללים. העדכונים יכלו לקרות רק על ידי הוראה מפורשת מפי המומחה.
בסופו של יום, הכיוון הזה לבניית AI גווע וכך גם ההתלהבות ממנו. היו לכך הרבה סיבות, ונזכיר רק אחת חשובה לענייננו, והיא בעיה טכנית כבדה: זה קשה מאד להושיב מומחים לתחום X ולבקש מהם שיכניסו את כל הידע הזה שיש להם לתוך המחשב. למה זה מסובך? קודם כל, כי ככל שמישהו מומחה יותר כך הוא גם עסוק יותר ומבוקש יותר, אז אין לו זמן. ושנית, הרבה מהידע הזה אינו ידע שכתוב באיזה ספר, או אפילו מנוסח בצורה מודעת בראש של המומחה. חלק מזה זה הרגלים, או נוהגים לא רשמיים שכולם בתחום מכירים אפילו שזה לא כתוב בשום מקום, וכן הלאה. בשורה התחתונה, העברת כל הידע למחשב היתה דבר שנשמע נחמד בתיאוריה, אבל בפועל היה מאד קשה לההתקדם בכיוון.
לאור הבעיה הזו, אפשר להבין את הכוח הפרגמטי של הגישה האינדוקטיבית בפתרון האתגר הזה: בגישה האינדוקטיבית, אין צורך להושיב מומחה מול המחשב, אלא אפשר פשוט לזרוק לתוך המחשב הרבה דאטה, והמחשב עצמו יחלץ את הכללים ממנו, בין אם הם כללים רשמיים ובין אם הם נרמזים מבין השורות. כמובן, הגישה הזו התאפשרה ברמה הפרקטית רק בגלל הרבה התפתחויות טכנולוגית חשובות שקרו בחמישים השנים האחרונות. קודם כל, הזמינות של המון המון דאטה מהמון המון סוגים היתה אבן דרך קריטית, שבין השאר נפתרה על ידי האינטרנט שהנגיש מאגרי נתונים חשובים לכל העולם. שינוי נוסף שקרה הוא ההתקדמות המטאורית בכוח המיחשוב וצניחה בעלויות שלו. רק כדי להמחיש עד כמה זה דרמטי, עשיתי בדיקה: שאלתי את GPT4 כמה זמן היה לוקח לאמן אותו אם היינו מנסים לעשות את זה עם טכנולוגיה של שנות ה-80 בלבד, אותם השנים שבהן מערכות המומחה כיכבו. התשובה שלו היתה: 2.7 מיליון שנה. בפועל, לקח לאמן אותו רק חצי שנה - אז תבינו איזו התקדמות טכנולוגית מטורפת קרתה כאן, ולמה יש דברים שגם אם פעם ידענו איך לעשות אותם על הנייר, הם נראו בלתי אפשריים בפועל ולכן לא קרו עד לאחרונה.
אלא שבד בבד עם התחכום שיש במערכת שלומדת לבד מהדאטה, נוצרה לנו בעיה חדשה. שכן כחלק בלתי נפרד מזה שהעצמנו אותה ונתנו לה יכולת ללמוד תבניות לבד מהדאטה, איבדנו על הדרך את הוודאות שאנחנו נוכל להבין בעצמנו את התבניות שהיא מחלצת מתוך הדאטה. כאן אנחנו בעצם נוגעים בתחום שלם שקוראים לו לפעמים AI Explainability, או "מובנותה של הבינה המלאכותית". חלק מהבעיה מגיעה ממה שראינו קודם, כשדיברנו על הביזור של המידע בין הרכיבים הרבים שמרכיבים את הקופסא השחורה שלנו, מה שמצריך חיבור פאזל לכדי סיפור שלם. עכשיו, אנחנו נראה עוד זווית של אותה הבעיה.
בואו נחשוב שוב על אפליקציית החתוליה שלנו. למה מראש חשבנו שבכלל אפשר לתכנת מחשב שיזהה אם יש או אין חתול בתמונה? אחת הסיבות הפשוטות לכך היא שבני אדם עושים את זה כל הזמן, אז כנראה שזה אפשרי. אנחנו מסתכלים בעזרת העיניים שלנו על תמונות, והמוח שלנו מסוגל לזהות אם יש שם חתול או לא. ואפילו אם פה ושם נטעה, בגדול אנחנו עושים עבודה ממש ממש טובה בזיהוי הזה.
אבל בו זמנית שאני משוכנע שזה אפשרי לתכנת, אם הייתם אומרים לי לנסח כללים שיסבירו איך אני יודע אם יש שם חתול או לא, לא נראה לי שהייתי מצליח. תזכרו שהכללים הללו צריכים לעבוד בתמונות שחור לבן כמו בתמונות בצבע; בזום-אין על הפרצוף של החתול או בזום אאוט כשרואים רק את הזנב שלו; צריך להתמודד עם זוויות צילום שונות וסוגי תאורה שונים, ומעל כל זה צריך להיות מסוגלים להבחין בין חתול לבין כלב לבין עכבר. כלומר, אפילו שאנחנו עושים את זה באופן אינטואטיבי, רובנו ואולי כולנו נתקשה להגדיר במדוייק מהם הכללים שהמוח משתמש בהם כדי להצליח לזהות חתולים. ולכן, כשאנחנו נותנים למכונה הלומדת לחלץ את התבניות הללו בעצמה, אנחנו נצטרך לאפשר למכונה מקסימום גמישות בזיהוי והגדרת הכללים הללו, כולל לצאת ממרחבים שאינטואטיבים לנו אל עבר הלא נודע, נכון? גם כללים שלנו נראים לא הגיוניים או אינטואטיבים, מבחינתנו היא יכולה להשתמש בהם אם זה ישיג את התוצאה הנדרשת של זיהוי חתולים.
כיוון שכך, כשהמכונה סוף סוף מצליחה לזהות חתולים, אם נבקש ממנה לספר לנו מהם הכללים שהיא מאמצת, זה לא יפתיע שיהיה לנו קשה להבין את התשובה שלה. לנו זה יראה, רוב הזמן, כאוסף גדול של מקרים ותגובות, במקום משהו אלגנטי כמו המשוואה המפורסמת של איינשטיין E=mc2. וכאן הקונטראסט למערכות מומחה מאד בולט: השפה של הכללים שם היתה שפה אנושית שמומחה כלשהו הכניס למערכת, ולכן היה לנו קל להבין עבור כל מקרה מה היה ההיגיון שהוביל להחלטה שלה. אבל עכשיו, במערכות הלומדות שתיארנו כאן, השפה שבה הכללים מנוסחים היא שפה שמחשב משתמש בה - מספרים ומשוואות. ממילא, זה מאד שכיח בעולמות ה-AI שאנשים מייצרים לעצמם מודלים מאד חזקים שמסוגלים לעשות המון דברים, כמו לזהות חתולים בתמונות, אבל שקשה מאד אפילו לאנשים הטכניים להבין מה הכללים שהמערכת משתמשת בהם בפועל. נכון, אפשר בהינף מקלדת לקבל את כל הנוסחאות שהמחשב משתמש בהן - אבל את המשמעות שלהן, למה דווקא הכללים הללו או הנוסחאות הללו עושות את הקסם הזה - את זה אין לנו דרך להבין רוב הזמן. הגישה שהמחשב יבחר בה כדי לגשת לפתרון בעיית זיהוי החתולים יכולה להיות שונה באופן קיצוני מגישה אנושית, כמו שציפורים ומטוסים עפים בצורות שונות מאד זו מזו. לנו יש אינטואיציות שמותאמות לנו, אבל הגמישות שנתנו בידי המחשב אומרת שהוא יכול להתכנס לכיוונים שמונחים על ידי אינטואיציה אחרת לגמרי, כזו שתהיה לנו קשה להבנה.
בואו נעמיק בבעיית המובנות כתוצאה מהשפה שהמחשב מאמץ, מעוד זווית, דוגמה שתיתן לעניין קונקרטיזציה מסויימת. דרך הדוגמה הזו אני מקווה שתבינו באופן חד יותר איך עודף הגמישות הזה שאנחנו נותנים למחשב יכול לייצר מערכת שתבלבל אותנו כשננסה להבין את הכללים שפיתחה. והדוגמה הזו היא ממערכת השמש.
כולנו בוודאי יודעים שהיו, לאורך ההיסטוריה, שתי גישות מרכזיות לתיאור האופן שבו גרמי השמיים נעים. הגישה הראשונה, שהתמסדה במאה הרביעית לפני הספירה על ידי אריסטו ותלמי, היתה הגישה הגיאוצנטרית, לפיה כדור הארץ נמצא במרכז היקום והשמש ושאר הפלנטות סובבות סביבו. הגישה השניה, שאותה פיתח קופרניקוס במאה ה-16 ושגלילאו תמך בה אפילו במחיר של עימות מול הכנסיה, היא זו שמקובלת כיום: הגישה ה"הליוצנטרית", לפיה השמש היא במרכז והפלנטות סובבות סביבה.
יש הרבה סיבות מדוע אנחנו מעדיפים כיום את הגישה ההליוצנטרית כתיאור נאמן ועדיף יותר מבחינה מדעית. אבל חשוב גם שנזכור שמבחינה מתמטית שתי האפשרויות הינן נכונות באותה מידה. כלומר, באותה מידה שאפשר לצייר את השמש במרכז ואז לצייר את תנועת הכוכבים והפלנטות סביבה, אפשר לעשות אותו הדבר כששמים את כדור הארץ במרכז, כנקודת הייחוס לכל החישובים שלנו. והאמת היא שכדור הארץ גם לא מיוחד בזה - כל נקודה ביקום שנבחר כנקודה ארכימדית, נקודה יציבה, ופשוט נפנה את המצלמה אל כל הגופים האחרים ביקום כפי שהם נראים מהזווית שלה - אפשר לתאר את התנועה שלהם ביחס לנקודה היציבה שבחרנו.
עכשיו, אם זה ככה, למה אנחנו מעדיפים את הגישה ההליוצנטרית? למה זה היה כל כך חשוב לגלילאו לבוא ולהגיד, בוא נעבור להסתכל על השמש כמרכז, ועל כל הפלנטות כסובבים את השמש? אחת התשובות העיקריות היא כי כשמסתכלים על הפלנטות ככה, הכל יותר אלגנטי ופשוט יותר לפירמול מתמטי. יש משהו במרכז, וכל הגופים האחרים עושים מסלול של מעגל, או יותר נכון אליפסה, סביב אותו מרכז. לעומת זאת, כאשר שמים את כדור הארץ במרכז ומציירים את תנועת הפלנטות, הם נראים כאילו הם מתחילים להשתולל. הם עדיין בסוף מסתובבים סביב כדור הארץ, אבל מסלולי התנועה שלהם מוזרים, שחלקם נראים כמו עלי כותרת של פרח, מתקרבים לכדור הארץ ואז מתרחקים באופן חד, ועוד כל מיני צורות מעניינות. במדע אנחנו אוהבים לומר שפשטות היא סימן לנכונות, שהיא כנראה משקפת איזשהו סדר יותר עמוק במציאות. ולכן אנחנו כבני אדם מעדיפים את האופציה ההליוצנטרית דווקא.
אבל - האם למחשב יש העדפה כזו? לא ממש. אם נציג למחשב את תנועת הכוכבים לאורך אלף שנה, ונבקש ממנו לבנות נוסחאות שאיתן נוכל לחזות את התנועה בעתיד, אין שום דבר שיחייב אותו להתכנס דווקא למודל ההליוצנטרי. הוא יכול ללמוד את התבניות מזוויות גיאוצנטרית באותה מידה. מרוב זה שהוא גמיש, מרוב זה שהוא יכול לבוא וללמוד חוקים חדשים וכללים חדשים ואיננו כבול לאינסטיקטים אנושיים של מה זו אלגנטיות מדעית, זה יכול לקרות.
כמובן, אולי לא אכפת לכם. אולי אתם מסתפקים בכך שיש לכם מכונה שדופקת עבודה ומצליחה לחזות את תנועת הכוכבים. אבל זה אך טבעי שיהיו כאלו שיגידו: אולי מתוך מבט על מה שהמכונה למדה נוכל לקבל תובנות על היקום? הרי היא מצליחה לחזות דברים מורכבים ביותר, אז בטח שם בפנים מחכה לה תובנה עסיסית או שתיים, לא?
אלא שכפי שאמרנו, באותה המידה שיכול להיות שתפתחו את מכסה המנוע ותגלו שם את המודל ההליוצנטרי האלגנטי, יכול להיות שתמצאו דווקא את המודל גיאוצנטרי, ולפיו כל פלנטה זזה קצת אחרת מהשניה, באופן שהוא מאד מבלבל ולא אינטואטיבי. בעוד המערכת הראשונה תלמד אותנו משהו על היקום, מהחשיפה למערכת השניה אנחנו נצא מבולבלים, כי לא היינו מצליחים להבין מה המסר, ולא היה ניתן להשליך את המודל שהיא חשפה למרחבים אחרים של ידע.
בואו נשווה את מה שאחנו אומרים כאן למה שדיברנו עליו בפרק שעבר, בסיפור עם האנס הנבון. שם, החשש שהעלינו היה שאולי מה שהמכונה למדה הוא טעות, או זיוף, כמו האנס האהוב שלנו שלמד לזהות שפת גוף ולא חילוק ארוך. אבל במקרה שלנו מדובר בבעיה דקה יותר ובמידה מסויימת מטרידה יותר: בשתי האפשרויות שתיארתי כאן המערכות הממוחשבות מדוייקות באותה מידה, וזיהו באותה מידה של דיוק את התבניות של גרמי השמיים. אף אחת מהן איננה זיוף או אשליה יותר מהשניה. אבל עדיין, באינטואיציה אנושית אחת מהן מספקת תובנות עומק זמינות לשימוש, בעוד השניה מספקת לנו רק בלאגן, בליל של כללים שאולי עובד בשטח אבל לא מעבר לזה. באופן אינטואטיבי אפשר אפילו לומר שאם היינו נוחתים על המודל הגיאוצנטרי, היינו קצת, בסתר ליבנו, מורדים במבחן טיורינג: היינו חשים, אני חושב, שלא רק מבחן התוצאה חשוב, אלא גם הדרך שמשיגים את התוצאה חשובה לא פחות.
אז בואו נתחיל לסכם. ראינו כאן איך המעבר מלמידה על ידי הוראה מפורשת מפי בני אדם, ללמידה עצמאית של המערכות הללו, פותרת סט אחד של בעיות ומייצרת סט אחר. באופן גס, אולי אפשר לומר שסט הבעיות שנפתר הינו סט בעיות הנדסי: איך לבנות מערכת מאד גמישה, שיכולה להתאים את הפעילות שלה להמון סיטואציות. אותה מערכת לזיהוי חתולים תוכל לזהות גם יצורים אחרים, הכל לפי כמות וסוג הדאטה שתיחשף אליו. אם נביא למערכת הרבה תמונות שבהן מסומנים ציפורי דרור, היא תזהה את ציפורי הדרור. מהרגע שהמערכת נבנתה, היא נתונה בידיו של המשתמש להחליט על איזה דאטה לאמן אותה ולאיזו מטרה.
אבל בד בבד שהבעיה ההנדסית נפתרה, נוצרה על הדרך בעיה אנאליטית: אפילו שאנחנו בנינו את המערכת, אנחנו פעמים רבות לא נוכל להסתכל עליה ולהבין למה ואיך היא מחליטה את הדברים שהיא מחליטה. כשנקבל פלט מהמערכת, אין לנו דרך לדעת למה דווקא פה זה מה שהיא החליטה. ולדבר הזה יש השלכות שחשובות לענייננו: קודם כל, זה קצת מקשה עלינו לענות על השאלה, האם המערכות הללו תבוניות? משהו בתוכנו היה מצפה לפתוח את מכסה המנוע, וכמו בסרטים שיזרח מבפנים אור לבן בוהק שימחיש שכן, נוצרה כאן תבונה, נוצר כאן מוח כמו המוח האנושי ואולי משהו שמעליו. אבל במקום זה אנחנו מקבלים משהו שנראה יותר כמו אוסף ענק של כללים שרירותיים, ואנחנו תוהים - אולי אין כאן דבר מלבד רשימה ארוכה ויבשה של מקרים ותגובות? גם אם המערכת הזו עוברת את מבחן טיורינג, זה מרגיש שהיא עוברת אותו באופן, איך נאמר, מאכזב. כמו כן, לחוסר המובנות של המערכת יש גם תופעות לוואי לא פשוטות, שכן תחשבו על השאלה - מי אחראי חוקית על הפעילות של מערכת שכזו? הבעלים שלה? מי שכתב את התוכנה? מי שאימן אותה? ככל שההבנה שלנו את מה שהיא עושה היא מוגבלת, כך קשה להגדיר את גבולות האחריות המשפטית שיש לכל צד בסיפור הזה.
אז זהו להיום! כמובן, חשוב לי לציין שתחום המובנות של AI הוא תחום מחקר נרחב, ולאורך זמן מדענים מצליחים לפענח חלקים ממה שמערכות ה-AI עושות בקישקעס שלהם. אבל הטיעון שניסיתי לפתח כאן היה לומר שכמעט תמיד אנחנו נהיה בפיגור גדול מאחורי הבנת המערכות הללו. אולי אני צודק, ואולי אני טועה - ימים יגידו! מה שחשוב הוא שעכשיו, בתקווה, יש לכם קצת יותר כלים אנאליטיים לדעת כיצד לגשת לנושא. הכלים הללו יוכלו לשמש אתכם וגם אותי ככל שהטכנולוגיה תתקדם, לבדוק האם משהו מהותי השתנה.
בכל אופן, בפעם הבאה אנחנו נסתכל על השאלה - איך מחשבים מבינים שפה, ואיך מספרים להם מה יש בתמונות? שני הדברים הללו, כפי שנראה, הם סופר קריטיים כדי לענות על השאלה שלנו האם מחשבים הם תבוניים, וזאת כי דרך שתי הנקודות הללו נבין גם חלק מהגאונות שבמערכות הללו, אבל גם נתחיל לראות איפה המטריקס של הבינה המלאכותית מסתיים והמציאות מתחילה. ועד אז…














Share this post